Per chiunque pensi che la geometria si concluda con l'analisi dei poligoni nello spazio, si sbaglia. Infatti, oltre la conoscenza comune e basilare dei tre assi cartesiani x, y e z, si estende un sapere molto più ambiguo e complesso. E' questo il punto in cui entra in gioco il V postulato di Euclide e le geometrie non euclidee, utilizzate anche in campo cosmologico. Vediamo di cosa si tratta.
Geometria euclidea: "Elementi" di Euclide
Prima di parlare delle geometrie euclidee, è necessario definire la geometria euclidea, ovvero quel modello geometrico descrittivo che abbiamo sempre utilizzato per analizzare la realtà che ci circonda e per risolverne i problemi.
La geometria euclidea, per come la intendiamo oggi, è un'evoluzione degli studi di geometria operati dal matematico greco Euclide, vissuto ad Alessandria intorno al 300 a.C. L’opera che racchiude in modo organico tutte le conoscenze acquisite dai Greci in secoli di ricerche è proprio “Elementi” di Euclide. Tra i 13 libri che la compongono, il più significativo per il nostro percorso è il primo, dove sono enunciate le basi della costruzione euclidea attraverso 23 termini, 5 postulati e 8 nozioni comuni.
Concentreremo la nostra attenzione sui postulati, dato che è proprio il V postulato a decretare la possibilità di passare dalle geometrie euclidee a quelle non euclidee.
5 postulati
Nell’intenzione di Euclide i postulati sono dotati di verità autoevidente, dunque sono accettabili sulla base dell’intuizione comune ed hanno un contenuto strettamente geometrico.
In ordine, lui definisce i postulati seguenti:
Si richiede che si possa condurre una linea retta da un qualsiasi punto a ogni altro punto (per due punti passa un segmento);
Si richiede che una retta terminata si possa prolungare continuamente per diritto (ogni segmento è estendibile a una retta);
Si richiede che si possa descrivere un cerchio con qualsiasi centro e ogni distanza (dato un centro e un raggio, esiste una circonferenza);
Si richiede che gli angoli retti siano uguali tra loro;
Si richiede che, se una retta venendo a cadere su due rette forma gli angoli interni e dalla stessa parte minori di due retti, le due rette prolungate illimitatamente verranno a incontrarsi da quella parte in cui sono gli angoli minori di due retti (se due rette tagliate da una trasversale formano da una parte di essa angoli coniugati interni la cui somma è minore di quella di due angoli retti, esse si incontrano da quella parte della trasversale).
Concentriamo la nostra attenzione sul V postulato, ovvero il discriminante ed il punto di partenza delle geometrie euclidee che si equivalgono alla geometria euclidea per la maggior parte di ciò che precede questo punto e si differenziano soprattutto per ciò che segue.
Il V postulato della geometria euclidea: dubbi ed enunciati
Euclide stesso, dopo aver definito in V postulato, osserva che c’è qualcosa che non funziona. La perplessità deriva essenzialmente da una sorta di esperimento logico riguardante le rette coinvolte nel postulato. Infatti, prese le rette r ed s, definisce P il punto in cui queste si incontrano in caso non fossero parallele e si accorge che, aumentando gradualmente l’angolo tra la retta r e la trasversale t, la somma degli angoli coniugati interni si avvicina sempre di più a due angoli retti. Questo sposta meccanicamente e senza controllo il punto P fino ad uscire dal foglio o, come diremmo noi oggi, lo farebbe tendere ad infinito.
I matematici greci in generale, coscienti dell’ambiguità, continuano i loro studi e derivano in particolare modo da esso alcuni enunciati non di poco conto che denotano ancora di più il divario con le geometrie non euclidee. Mi riferisco ai seguenti:
Teorema dell’unicità della parallela: dati una retta r e un punto P esterno ad essa, esiste una e una sola retta passante per P e parallela ad r;
Due rette parallele sono equidistanti;
La somma degli angoli interni di un triangolo è uguale a due angoli retti (più in generale, la somma degli angoli interni di un poligono di n lati è il risultato dell’operazione 180°(n-2));
Triangoli simili non uguali: dato un triangolo qualsiasi, se ne può costruire un altro ad esso simile (cioè con gli stessi angoli) di lato assegnato;
Teorema di Pitagora: in un triangolo rettangolo, il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Geometrie non euclidee: modelli a confronto
A partire dall’ambiguità del V postulato sono nati nuovi modelli geometrici che hanno reinterpretato le relazioni che intercorrono tra gli alimenti semplici in maniere del tutto differenti, arrivando anche a conclusioni opposte. Le nuove geometrie ad essere nate sono state tante, alcuni esempi sono
geometria iperbolica;
geometria ellittica;
geometria sferica;
geometria proiettiva;
geometria della gomma;
ecc...
Quelle che più comunemente si analizzano sono quella iperbolica ed ellittica, che si possono confrontare con la geometria euclidea consultando la seguente tabella che include gli enunciati derivati dal V postulato:
| Iperbolica | Euclidea | Ellittica |
Unicità parallele | Infinite | Unica | Nessuna |
Somma angoli interni triangolo | < 180° | = 180° | > 180° |
Triangoli simili | Uguali | Non uguali | Uguali |
Teorema di Pitagora |  |  |  |
Anche se in un linguaggio matematico è difficile capire cosa queste conseguenze comportano, la "rivoluzione geometrica" risulta ancora più sconvolgente quando si cerca di visualizzare la teoria in uno spazio pratico. Online sono disponibili vari video di simulazioni virtuali in cui lo spazio segue delle geometrie non euclidee in grado di farci girare la testa (esempio: Non-euclidean virtual reality). Di seguito alcune immagini per dare un'idea dei modelli descrittivi della realtà che stiamo approcciando:
Le geometrie non euclidee in cosmologia: la forma ed il destino dell’universo
Anche se non ce lo aspetteremmo, la realtà in cui viviamo non segue necessariamente la geometria euclidea che siamo abituati a sperimentare. Infatti, nel corso degli anni gli scienziati cosmologi hanno cercato di studiare le informazioni provenienti dall’universo, in particolare la radiazione cosmica di fondo, per comprendere quale fosse la forma del nostro universo. Le ipotesi di partenza prevedevano anche modelli di geometrie non euclidee in base al valore di densità di materia (ρ) riscontrato rispetto ad un valore base, chiamato densità critica (ρc):
Universo aperto | Universo piatto | Universo chiuso |
Geometria iperbolica | Geometria euclidea | Geometria sferica (ellittica) |
ρ < ρc  | ρ = ρc | ρ > ρc  |
Curvatura negativa | Curvatura nulla | Curvatura positiva |
Estensione infinita  | .  | Estensione finita  |
Espansione infinita, ma più | lenta (no energia oscura) | Big Crunch |
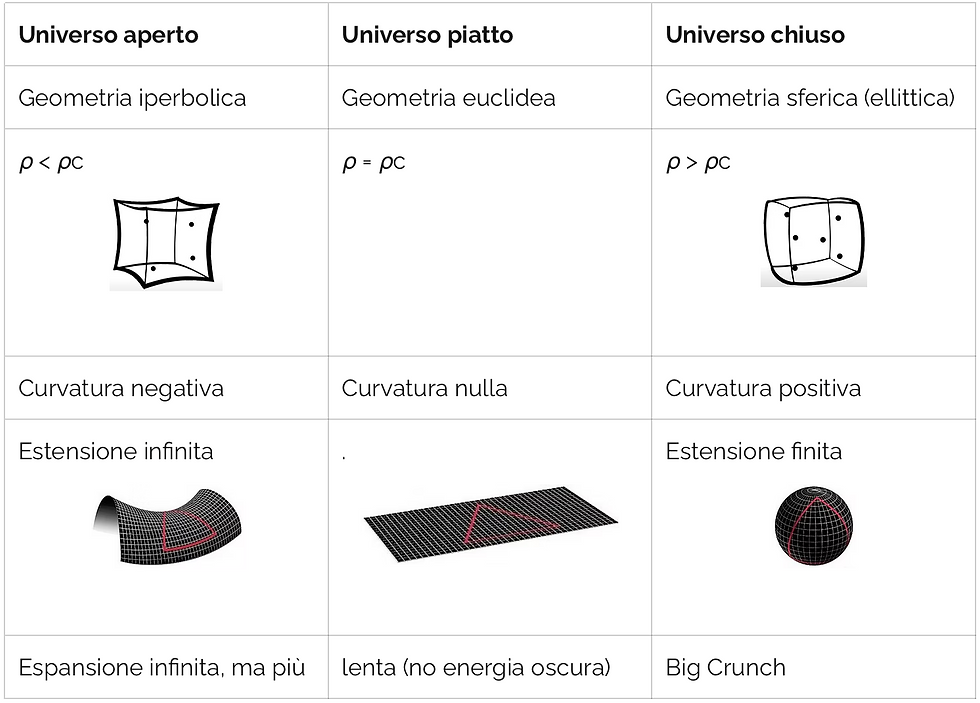
Sperimentalmente, grazie allo studio dei dati della radiazione cosmica di fondo, si è appurato che la densità dell’universo è pari alla densità critica e, per questo motivo, il nostro universo ha geometria piatta, piana, euclidea.
In realtà, il dibattito è ancora aperto, perché le nostre misurazioni riguardano l’universo da noi osservabile, il quale non coincide con l’universo per intero ma ne è solo una parte. Facciamo un esempio: se un uomo comune che si trova sulla terra dovesse definire la forma del nostro pianeta, nella sua ingenuità e limitatezza direbbe che la terra è piatta. Anche noi, nella stessa maniera, essendo costretti a considerare solo l’universo da noi osservabile, potremmo star commettendo un errore, perché analizziamo le caratteristiche di una porzione di un intero immenso che ci potrebbe trarre in inganno.
Al prossimo articolo!
L(&A)
Commentaires